Programación Lineal. Resolución gráfica
Rectas:
Dispones de 6 rectas predefinidas. Con el botón
secundario
del ratón pueden modificarse sus parámetros o eliminarse si sobra
alguna.
Si se necesita alguna recta más, puede añadirse escribiendo su ecuación
en la barra de abajo. Ejemplo: r8: 4x-2y = 4
Puntos:
Los puntos de corte de las rectas también pueden modificarse, borrarse
o añadir alguno más. Ejemplo: D = Interseca[r1,r5].
Para ver las coordenadas: 'Propiedades de objeto /
Muestra rótulo: Nombre y valor'.
Función a optimizar:
También hay que cambiar sus parámetros para adaptarlos al problema que
se esté haciendo.
Vector y recta auxiliar:
Al mover el punto P se va moviendo una recta paralela al vector que
dirige la función a optimizar.
Conforme se mueve el punto P, se va moviendo el punto S, que nos dará
el valor óptimo de la función F.
Regiones:
Usando la herramienta 'Polígono' 
podrían dibujarse las regiones de validez de cada
recta.
Si la aplicación no funciona desde internet, descarga este archivo y lo abres con el programa geogebra
PROBLEMA:
Con el comienzo del curso se van a lanzar unas ofertas de material
escolar. Unos almacenes quieren ofrecer 600 cuadernos, 500 carpetas y
400 bolígrafos para la oferta, empaquetándolo de dos formas distintas;
en el primer bloque pondrá 2 cuadernos, 1 carpeta y 2 bolígrafos; en el
segundo, pondrán 3 cuadernos, 1 carpeta y 1 bolígrafo. Los precios de
cada paquete serán 6.5 y 7 €, respectivamente. ¿Cuántos paquetes le
conviene poner de cada tipo para obtener el máximo beneficio?
SOLUCIÓN:
Elección de las incógnitas.
x = nº de paquetes del primer tipo
y = nº de paquetes del segundo tipo
Función objetivo
F(x, y) = 6.5x + 7y
Restricciones
| Cantidad |
Cuadernos |
Carpetas |
Bolígrafos |
|
| P1 |
x |
2x |
x |
2x |
| P2 |
y |
3x |
y |
y |
| Disponibles |
600 |
500 |
400 |
Carpetas: x + y ≤ 500
Bolígrafos: 2x + y ≤ 400
x ≥ 0
y ≥ 0
Ya lo tenemos preparado. Se modifica en la aplicación la función F, las rectas r1, r2 y r3 y se eliminan las r4 y r5. Se redefinen los puntos de corte, añadiendo el D, y se dibuja la región de aceptación. Se modican también las coordenadas del vector director de F.
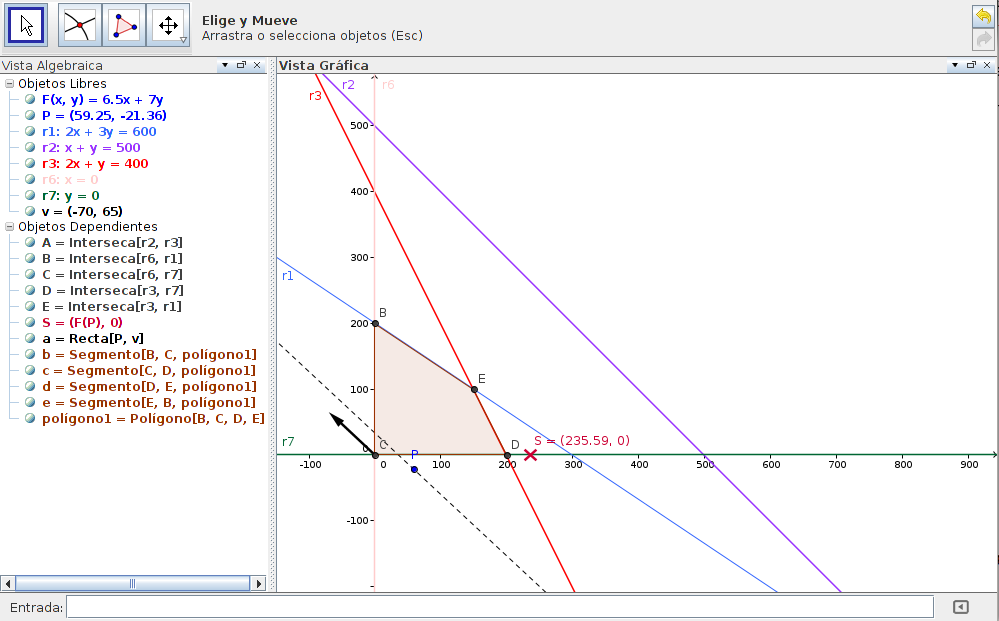
Se mueve a mano el punto P y se observa que el máximo se alcanzará en E. Mostramos sus coordenadas con 'Propiedades de objeto / Muestra rótulo: Nombre y valor'. Se modifican las coordenadas de P para que coincidan con las del punto E.
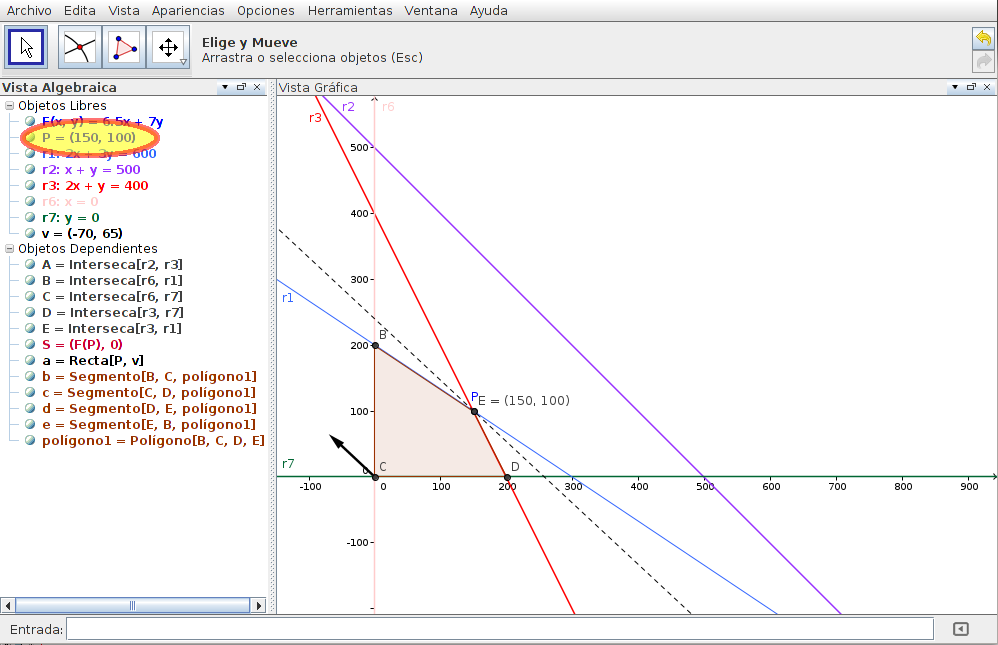
No se ve el punto S, que tiene la solución máxima para la función F. Se usa la herremienta de zoom para alejar el gráfico.
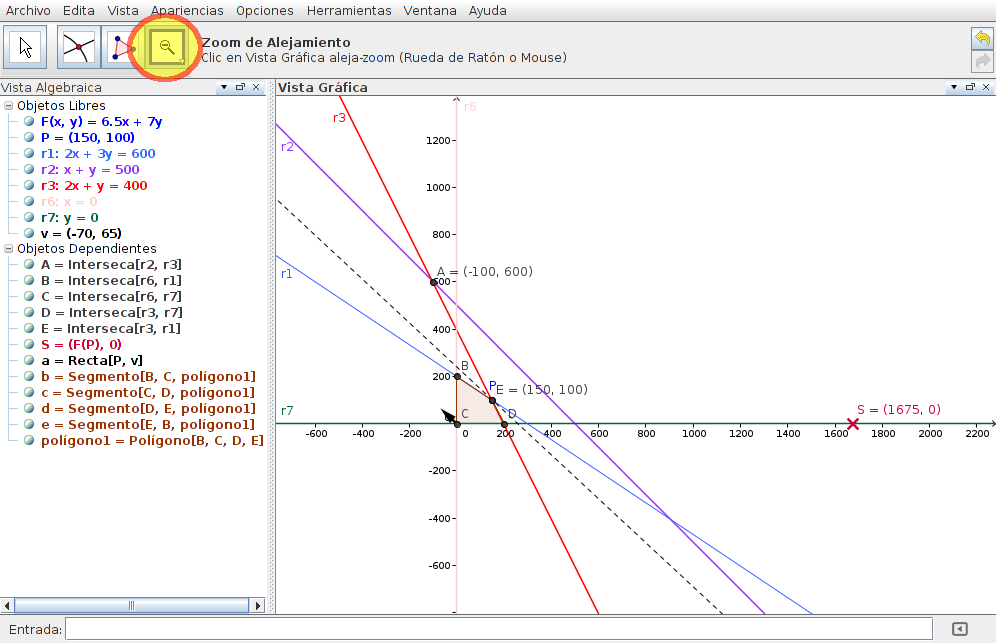
En este problema la solución es 150 lotes de tipo P1 y 100 de P2, con un beneficio de 1675€
Paco Muñoz, Creado con GeoGebra